2015年北京数学理科试题及答案word在线版[二]
2015北京理科数学第二部分(非选择题 共110分)
二、填空题共6小题,每小题5分,共30分.
9.在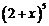 的展开式中,
的展开式中,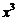 的系数为 .(用数字作答)
的系数为 .(用数字作答)
10.已知双曲线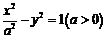 的一条渐近线为
的一条渐近线为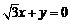 ,则
,则 .
.
11.在极坐标系中,点 到直线
到直线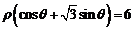 的距离为 .
的距离为 .
12.在 中,
中, ,
,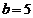 ,
, ,则
,则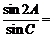 .
.
13.在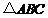 中,点
中,点 ,
, 满足
满足 ,
, .若
.若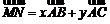 ,则
,则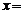 ;
;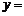 .
.
14.设函数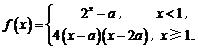
①若 ,则
,则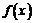 的最小值为 ;
的最小值为 ;
②若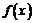 恰有2个零点,则实数
恰有2个零点,则实数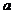 的取值范围是 .
的取值范围是 .
三、解答题(共6小题,共80分.解答应写出文字说明,演算步骤或证明过程)
15.(本小题13分)
已知函数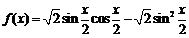 .
.
(Ⅰ) 求 的最小正周期;
的最小正周期;
(Ⅱ) 求 在区间
在区间 上的最小值.
上的最小值.
16.(本小题13分)
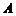 ,
, 两组各有7位病人,他们服用某种药物后的康复时间(单位:天)记录如下:
两组各有7位病人,他们服用某种药物后的康复时间(单位:天)记录如下:
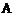 组:10,11,12,13,14,15,16
组:10,11,12,13,14,15,16
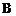 组:12,13,15,16,17,14,
组:12,13,15,16,17,14,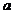
假设所有病人的康复时间互相独立,从 ,
,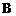 两组随机各选1人,
两组随机各选1人,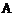 组选出的人记为甲,
组选出的人记为甲, 组选出的人记为乙.
组选出的人记为乙.
(Ⅰ) 求甲的康复时间不少于14天的概率;
 (Ⅱ) 如果
(Ⅱ) 如果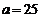 ,求甲的康复时间比乙的康复时间长的概率;
,求甲的康复时间比乙的康复时间长的概率;
(Ⅲ) 当 为何值时,
为何值时, ,
,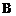 两组病人康复时间的方差相等?(结论不要求证明)
两组病人康复时间的方差相等?(结论不要求证明)
17.(本小题14分)
如图,在四棱锥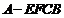 中,
中, 为等边三角形,平面
为等边三角形,平面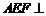 平面
平面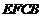 ,
,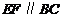 ,
,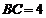 ,
,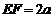 ,
,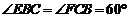 ,
,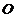 为
为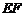 的中点.
的中点.
(Ⅰ) 求证: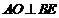 ;
;
(Ⅱ) 求二面角 的余弦值;
的余弦值;
(Ⅲ) 若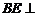 平面
平面 ,求
,求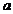 的值.
的值.
18.(本小题13分)
已知函数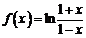 .
.
(Ⅰ)求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)求证:当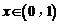 时,
时, ;
;
(Ⅲ)设实数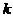 使得
使得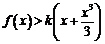 对
对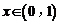 恒成立,求
恒成立,求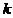 的最大值.
的最大值.
19.(本小题14分)
已知椭圆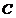 :
: 的离心率为
的离心率为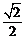 ,点
,点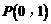 和点
和点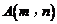
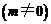 都在椭圆
都在椭圆 上,直线
上,直线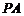 交
交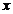 轴于点
轴于点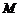 .
.
(Ⅰ)求椭圆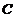 的方程,并求点
的方程,并求点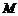 的坐标(用
的坐标(用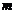 ,
,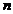 表示);
表示);
(Ⅱ)设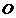 为原点,点
为原点,点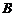 与点
与点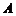 关于
关于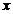 轴对称,直线
轴对称,直线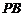 交
交 轴于点
轴于点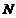 .问:
.问: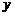 轴上是否存在点
轴上是否存在点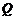 ,使得
,使得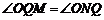 ?若存在,求点
?若存在,求点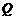 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
20.(本小题13分)
已知数列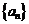 满足:
满足: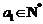 ,
,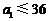 ,且
,且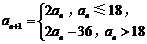
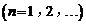 .
.
记集合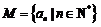 .
.
(Ⅰ)若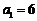 ,写出集合
,写出集合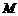 的所有元素;
的所有元素;
(Ⅱ)若集合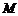 存在一个元素是3的倍数,证明:
存在一个元素是3的倍数,证明: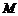 的所有元素都是3的倍数;
的所有元素都是3的倍数;
(Ⅲ)求集合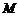 的元素个数的最大值.
的元素个数的最大值.
(文章来源招生考试网,转载请注明原文出处: https://www.sczsxx.com/html/gaokaoziyuan/liniangaokaoshiti/2015/0609/119541.html)
- 热门内容



